
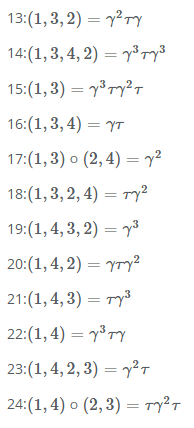
En reprenant les dénominations des 24 éléments ci-dessus alors:
Ce groupe possède 30 sous-groupes:
1 d'ordre 1 le groupe trivial, il s'agit du sous-groupe: {1}
_________________________________
9 d'ordre 2 isomorphes à Z/2Z (groupes cycliques) ce sont les sous-groupes:
{1,2},{1,3},{1,6},{1,7},{1,8},{1,15},{1,17},{1,22},{1,24}
_________________________________
4 d'ordre 3 isomorphes à Z/3Z (groupes cycliques) ce sont les sous-groupes:
{1,4,5},{1,9,13},{1,16,21},{1,12,20}
_________________________________
7 d'ordre 4 répartis selon:
3 isomorphes à Z/4Z (groupes cycliques) ce sont les sous-groupes:
{1,8,18,23},{1,10,17,19},{1,11,14,24}
4 isomorphes à V4 le groupe de Klein ce sont les groupes:
{1,2,8,7},{1,3,22,24},{1,6,15,17},{1,8,17,24}
_________________________________
4 d'ordre 6 isomorphes au groupe symétrique S3 ce sont les sous-groupes:
{1,3,7,9,13,15},{1,6,7,12,20,22},{1,2,15,16,21,22},{1,2,3,4,5,6}
_________________________________
3 d'ordre 8 isomorphes au groupe diédral D8 ce sont les sous-groupes:
{1,2,7,8,17,18,23,24},{1,6,8,10,15,17,19,24},{1,3,8,11,14,17,22,24}
_________________________________
1 d'ordre 12 isomorphe au groupe alterné A4 il s'agit du sous-groupe:
{1,4,5,8,9,12,13,16,17,20,21,24}
_________________________________
1 d'ordre 24 le groupe S4 lui même
_________________________________
_________________________________
Sur ces 30 sous-groupes, 4 sont normaux:
Le premier : {1}
Le deuxième : {{1},(1,2)o(3,4),(1,3)o(2,4),(1,4)o(2,3)} qui est le sous-groupe {1,8,17,24}
Le troisième : A4 le groupe alterné
Le quatrième : S4
________________________________
________________________________
S4 possède 5 classes de conjugaison
La première : {1}
La deuxième : {8,17,24}
La troisième : {2,3,6,7,15,22}
La quatrième : {10,11,14,18,19,23}
La cinquième : {4,5,9,12,13,16,20,21}
Ce groupe symétrique permet de redécouvrir le birapport harmonique
Nous regarderont donc ce qu'il en est...