division harmonique de Breuil
Posté : 07 sept.25, 19:35
Issue de ce résultat dans ce lien https://les-mathematiques.net/vanilla/d ... diculaires
Dans l'image ci-dessous on y voit un triangle A'B'C' directement semblable au triangle ABC
Une droite de couleur vert clair qu'on appellera la droite principale de Breuil
Une droite de couleur vert foncée qu'on appellera droite secondaire de Breuil
Ce triangle A'B'C' comme ces deux droites n'ont pas étés choisis au hasard et on peut les deviner en complétant la figure donnée dans ce lien en effectuant la construction proposée sur les trois côtés de ce triangle ABC
Deux hyperboles équilatères
L'une de couleur rouge est circonscrite au triangle ABC et est la transformée isogonale de la droite principale de Breuil par rapport au triangle ABC
L'autre de couleur violet est circonscrite au triangle A'B'C' et est la transformée isogonale de la droite principale de Breuil par rapport au triangle A'B'C'
Cette droite principale de breuil est tangente à ces deux hyperboles
On y devine aussi deux quadrilatères complets et une certaine division harmonique sur la droite secondaire de Breuil (titre de ce sujet)
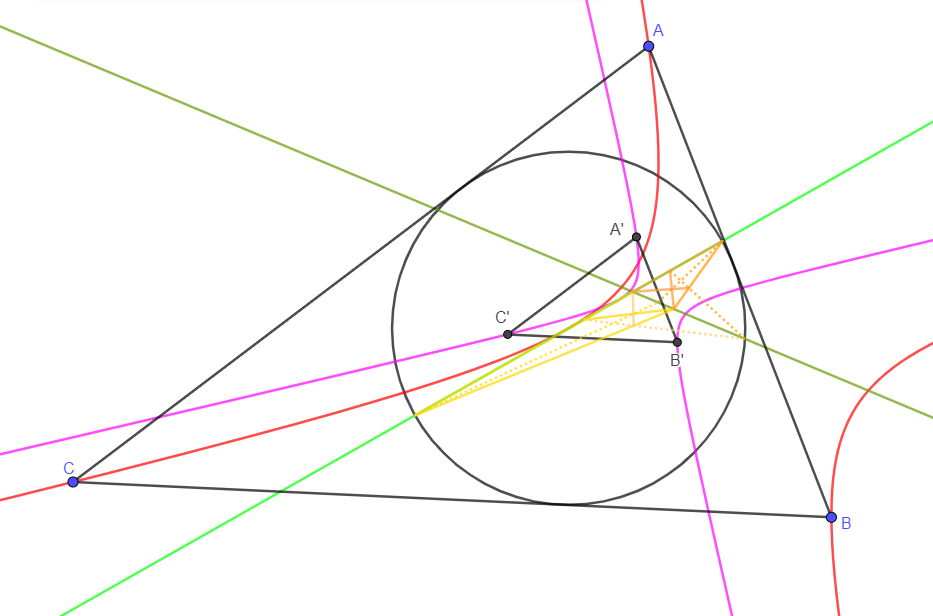
Dans l'image ci-dessous on y voit un triangle A'B'C' directement semblable au triangle ABC
Une droite de couleur vert clair qu'on appellera la droite principale de Breuil
Une droite de couleur vert foncée qu'on appellera droite secondaire de Breuil
Ce triangle A'B'C' comme ces deux droites n'ont pas étés choisis au hasard et on peut les deviner en complétant la figure donnée dans ce lien en effectuant la construction proposée sur les trois côtés de ce triangle ABC
Deux hyperboles équilatères
L'une de couleur rouge est circonscrite au triangle ABC et est la transformée isogonale de la droite principale de Breuil par rapport au triangle ABC
L'autre de couleur violet est circonscrite au triangle A'B'C' et est la transformée isogonale de la droite principale de Breuil par rapport au triangle A'B'C'
Cette droite principale de breuil est tangente à ces deux hyperboles
On y devine aussi deux quadrilatères complets et une certaine division harmonique sur la droite secondaire de Breuil (titre de ce sujet)
