Religions du monde :: forum religion

Bon ce sujet intéresse J'm'interroge
On cherche à écrire un polynôme à coefficients dans l'ensemble des rationnels (lorsque t et u sont rationnels) tel qu'une de ses racines soit le rayon du cercle (alpha)
Cette écriture sera normalement réalisée avant la fin de l'année 2025
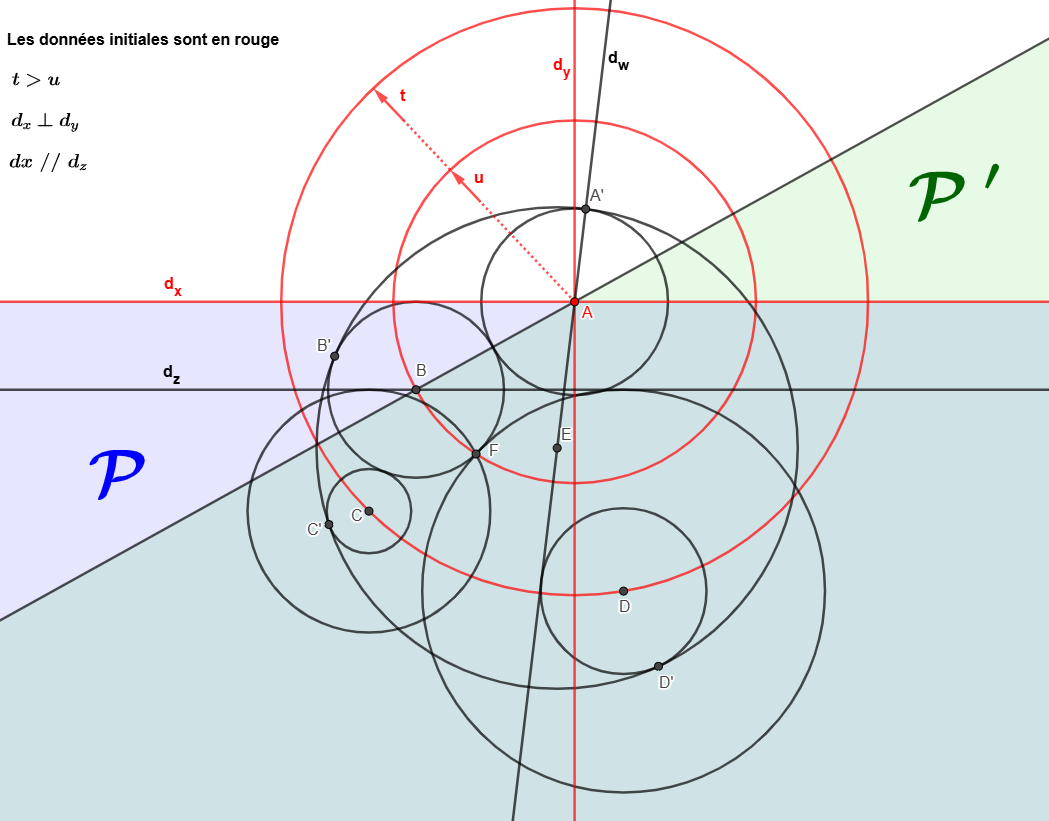
Voici ci-dessous l'énoncé géométrique et la figure

.
C'était bien comme cela que je l'avais visualisé.

Les figures traçables, mais non constructibles sont un sujet de réflexion intéressant, en effet.
.

mince faudra que je refasse le texte
J'ai oublié de dire que la droite dx est une tangente du cercle beta

sinon à part cela même si l'image semble le montrer car le grossissement ne permet pas bien de le voir les cercles alpha et le cercle de centre D passant par F ne sont pas forcément extérieurement tangents
Ce n'est pas dans les contraintes (ce n'est pas un oubli)

J'm'interroge a écrit : 06 déc.25, 23:18 Les figures traçables, mais non constructibles sont un sujet de réflexion intéressant, en effet.

L’empirie peut révéler des objets ou des structures que les cadres formels ne savent pas produire, dévoilant un écart entre ce qui apparaît et ce qui est justifiable. Les algorithmes fournissent des procédures explicites : ils délimitent ce qui est admis dans une perspective constructiviste. La logique constructiviste exige une construction formelle explicite pour reconnaître une existence et rejette les preuves indirectes ou fondées sur la seule cohérence.

La logique classique adopte une autre norme : elle accepte l’existence dès qu’une preuve, même non constructive, garantit la cohérence du système. La cohérence devient alors le critère : si la négation conduit à une contradiction, l’existence est affirmée, même sans procédé.

Les figures non constructibles de manière explicitement formelles mettent en évidence ce contraste. Même lorsqu'elles peuvent être produites empiriquement, elles restent exclues du constructivisme faute de pouvoir l'être formellement par des opérations autorisées.

L’empirisme et la logique classique ne s’excluent pas : l’un fournit ce qui est constaté, l’autre en assure la légitimité théorique. La tension apparaît lorsque l’on interroge ce qui est réellement connaissable : faut-il le fonder sur la cohérence ou sur la possibilité d'en rendre compte par une preuve constructive ? C’est là que se joue une part centrale de la réflexion épistémologique.
.

Je n'ai rien compris J'm'interroge (comme tu le sais moi et la logique c'est difficile)
Merci d'avoir participé à mon sujet
Tiens pour la peine je t'offre une couleur (sauf la noire car je me suis déjà servi désolé)
Any Colour You Like https://www.youtube.com/watch?v=l8pEjmZVx3k

aerobase a écrit : 07 déc.25, 21:07 Any Colour You Like https://www.youtube.com/watch?v=l8pEjmZVx3k

Ah le synthé p[gros mot]n !

J'aurai un peu de retard pour ma proposition de polynôme (il n'est évidemment pas unique) J'm'interroge

ça se fera avant fin janvier plutôt que fin décembre bref...